对抗样本与防御
|
1,717
|
0
|
Others
|

4647 字
|
29 分钟

零 前言

在利益驱动的黑产领域，技术的更新迭代和高度自动化攻击超乎常人想象。在2017年，腾讯守护者计划安全团队协助警方打掉市面上最大打码平台“快啊答题”，挖掘出一条从撞库盗号、破解验证码到贩卖公民信息、实施网络诈骗的全链条黑产。而在识别验证码这一关键环节，黑产竟已用上AI人工智能技术。该团伙运用AI技术训练机器，极大提升了单位时间内识别验证码的数量，2017年一季度打码量达到259亿次，且识别验证码的精准度超过80%。

在继续使用图形验证码来进行机器人验证的前提下，可以利用深度学习的脆弱性，以对抗样本的攻击方式来降低攻击者的识别精准度和成本。利用深度学习脆弱性的攻击方式还有:

  1. 偷取模型
  2. 数据投毒

该文，将从以下几点，对对抗样本与防御进行探究与学习:

  • 基础知识
  • 对抗样本的算法
  • 防御方法

若文中有什么错误或问题，还望各位批评指正。

一 基础知识

1. 基本过程

我们从单神经元神经网络入手。

(1) 预测与检验

预测函数:

$z = dot(w,x)+b ==> z = {w^T}x + b$

$dot()$ 函数表示 向量相乘

$x$ 表示 输入特征向量

$w$ 表示特征的权重

$b$ 阈值,用于影响预测

理解与举例说明:

周末，你想出去玩。预测函数，对你是否决定出去玩进行预测。当前情况下，有三个输入特征，分为$x_1,x_2,x_3$,权重依次为$w_1,w_2,w_3$,设置阈值$b = -5$，$z > 0$ 表示你会出去玩。

假设你有考试，输入特征和权重为

$$
(x_1,x_2,x_3) = (0,0,1)
(w_1,w_2,w_3) = (1,1,2)
$$
那么$ z = 0* 1 + 0* 1 + 1* 2+ (-5)= -3$，则预测表示你不会出去玩。

激活函数

此外，因为上面的预测函数只是单一的线性函数，为了解决更多问题，我们还需要添加非线性的激活函数。

如，sigmoid函数. $\sigma(z) = \frac{1}{1+e^{-z}}$

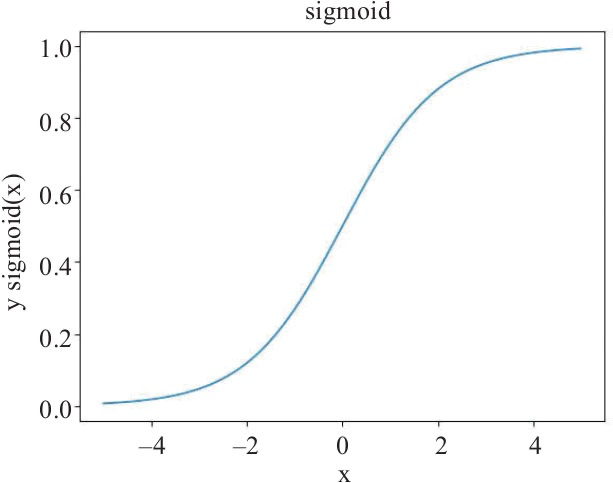
image-20210615000902705

$\hat{y}^{(i)} = \sigma({w^T} {x^{(i)}} + b) $,其中 $i$ 表示某一训练样本,$\hat{y}^{(i)}$为该结果

image-20210614232205515

同时由上面的公式，我们可以很清晰的理解到：预测的精确度取决于$w,b$。

验证成果

损失函数 (loss function),用于计算预测结果是否准确。 $L(\hat{y}^{(i)} ,y^{(i)})$
理论上，可以用以下函数进行计算
$$
L(\hat{y}^{(i)} , y^{(i)}) = \frac{1}{2}(\hat{y}^{(i)} – y^{(i)} )^2
$$

实际过程中，会更加复杂
$$
L(\hat{y}^{(i)} , y^{(i)}) = -(y \, log(\hat{y}^{(i)}) + (1-y)\, log(1-\hat{y}^{(i)}))
$$

损失函数是可以很好的反映模型与实际数据差距的工具,理解损失函数能够更好的对后续优化工具(梯度下降、对抗样本等)进行分析与理解。

针对整个训练集的损失函数，我们称为成本函数,其本质上是对每个样本的损失函数进行累加，然后求平均值。
$$
J(w,b) =\frac{1}{m}\sum_{i=1}^m L(\hat{y}^{(i)} , y^{(i)})
$$

(2) 学习过程

理解学习过程，将对理解神经网络原理和对抗样本攻击都十分有益。

由预测与检验一节，我们得知预测的精确度取决于$w,b$，而神经网络学习的目的就是找到合适的$w,b$.

$$
\hat{y}^{(i)} = \sigma({w^T} {x^{(i)}} + b), \sigma(z) = \frac{1}{1+e^{-z}}\
J(w,b) =\frac{1}{m}\sum_{i=1}^m L(\hat{y}^{(i)} , y^{(i)}) = – \frac{1}{m}\sum_{i=1}^m {y}^{(i)}log \, \hat{y}^{(i)} +(1 – {y}^{(i)}) \, log(1-\hat{y}^{(i)})
$$
下面图片表示的是损失函数$J(w,b) $

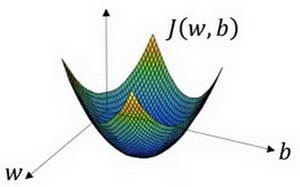
a3c81d2c8629d674141def47dc02f312

可以看出损失函数 J 为向下凸起的函数。

梯度下降算法

为找到合适的$w,b$,以及降低损失函数，我们采用梯度下降算法。

假定代价函数 𝐽(𝑤)J(w) 只有一个参数 𝑤w，即用一维曲线代替多维曲线。如下图所示。

5300d40870ec58cb0b8162747b9559b9

首先，对$w_0$ 取初始值，之后进行计算，得到预测值和损失 $J(w_0)$。

之后对损失函数关于$w$对求导，得到$\mathrm{d}w $ (即为 $\mathrm{d}J / \mathrm{d}w $)

利用$\mathrm{d}w$对$w$进行更新,$w\prime = w – r * \mathrm{d}w$，其中$r$表示为学习率，可以理解为每次下降的步长。

得到新的$w$，再一次进行计算损失和损失函数，若没有得到目标(损失小于一定值)，则对上面的流程再来一次。

(3) 计算图

神经网络的计算是由一个前向传播以及一个反向传播构成的。先通过前向传播计算出预测结果以及损失;然后再通过反向传播计算岀损失函数关于每一个参数(W、b)的偏导数并对这些参数进行梯度下降,然后用新的参数进行新一轮的前向传播计算,这样来回不停地进行前向传播反向传播计算来训练(更新)参数使损失函数越来越小使预测越来越精准。

前向传播

假设前向传播如下:
$$
z = {w^T}x + b\
\hat{y} = a = \sigma({w^T} x + b) \
L(a , y = -(y \, log(a) + (1-y)\, log(1-a))
$$
计算图如下:

image-20210617011733679

反向传播

经过链式计算得
$$
\mathrm{d}w_1 = x_1 \mathrm{d}z\
\mathrm{d}w_2 =\mathrm{d}z\
\mathrm{d}b = \mathrm{d}z\
\mathrm{d}z = a -y\
$$
设置好学习率$r$，后利用$ \mathrm{d}w_1, \mathrm{d}w_2, \mathrm{d}b$进行梯度下降，更新参数，再次前向传播然后再反向传播，通过这样不停的前向反向传播来训练参数，直到达到目的。

二 对抗样本

抗样本按照攻击成本可以分为白盒攻击、黑盒攻击和物理攻击，按照攻击目标分为定向攻击和无定向攻击。白盒攻击需要完整获取模型，了解模型的结构以及每层的具体参数，可以完全控制模型的输入，对输入数据甚至可以进行比特级别的修改。相对于黑盒攻击和物理攻击，白盒攻击的研究更加成熟。

白盒攻击

基本原理

从数学角度描述对抗样本，输入数据为x,分类器为$f$,对应的分类结果表示为$f(x)$ 。假设存在一个很小的$\varepsilon$，使得:

$$
f(x + \varepsilon) ! = f(x)
$$

以例子说明:

n_features = 1000 # 表示每个样本的特征数
n_samples = 4000 # 表示生成的样本数量
n_classes = 2 # 表示 生成样本对应的标签种类数量
random_state = 0 # 随机种子值
x, y = datasets.make_classification(n_samples=n_samples, n_features=n_features, n_classes=n_classes, random_state=random_state)

# 转换成one hot编码[0 1] [1 0]
y = to_categorical(y)
# 标准化到0-1之间
x = MinMaxScaler().fit_transform(x)

使用的分类模型是一个非常简单的多层感知机，输入层大小为1000，输出层为2，激活函数为softmax

model = Sequential()
model.add(Dense(2, activation='softmax',
                input_shape=(n_features,)))
model.compile(loss='categorical_crossentropy',
              optimizer=RMSprop(),
              metrics=['accuracy'])

model.summary() # 打印模型的结构

进行训练，批大小为16，训练30轮，准确度稳定在86%

model.fit(x,y,epochs=30,batch_size=16)
image-20210617025957426

对第0号数据进行预测，结果如下图, 预测结果为标签0

image-20210617030848366
x0=x[0]
y0=y[0]
x0 = np.expand_dims(x0, axis=0)
y0_predict = model.predict(x0)

index=[0,1]
labels=["lable 0","lable 1"]
probability=y0_predict[0]

在第0号数据的每一个特征上都叠加一个0.01或者-0.01的扰动生成新的数据，再对新数据进行预测，发现结果为标签1

image-20210617030900389
e = 0.01
cost, gradients = grab_cost_and_gradients_from_model([x0, 0])
n = np.sign(gradients)
x0 += n * e
#print(x0)
y0_predict = model.predict(x0)
print("new_y0_predict",y0_predict)

0.01还是-0.01取决于n = np.sign(gradients) x0 += n * e，即取决反向传播得到导数的方向，从而使损失增大。

基于优化的对抗样本生成攻击

深度学习在训练过程中，通过计算样本数据的预测值与真实值之间的损失函数，之后在反向传递的过程中通过链式法则调整模型的参数，不断减小损失函数的值，迭代计算出模型的各层参数。

攻击原理

image-20210617031707098

生成对抗样本的基本过程也可以参考这一过程，不同的是在迭代训练的过程中，我们把网络的参数固定下来，把对抗样本当作唯一需要训练的参数，通过反向传递过程调整对抗样本。

image-20210617031744870

生成对抗样本

在示例中，通过损失函数在反向传递过程中直接调整原始图像的值，直到满足最大迭代次数或者对抗样本预测值达到预期为止。

image-20210617032051946

示例中的模型为公开的Alexnet，是基于

加载经典的熊猫图片并进行标准化处理。OpenCV默认加载图片的方式是BGR格式而不是RGB格式，需要手工进行转换。攻击的对象是Alexnet，对应的预训练模型是基于ImageNet 2012数据集进行训练的，因此对数据进行标准化时，不能简单地进行归一化处理，而是需要使用特定的均值mean和标准差std。另外需要强调的是，OpenCV默认保存图片时使用的是WHC格式，即第三个维度是通道数据，比如本例中为[224，224，3]，但是PyTorch是CWH格式，因此需要转换成[3，224，224]，这一过程是调用img.transpose完成的。

# 图像加载以及预处理 
    image_path = "picture/cropped_panda.jpg"
    orig = cv2.imread(image_path)[..., ::-1]
    orig = cv2.resize(orig, (224, 224))
    img = orig.copy().astype(np.float32)

    mean = [0.485, 0.456, 0.406]
    std = [0.229, 0.224, 0.225]
    img /= 255.0
    img = (img - mean) / std
    img = img.transpose(2, 0, 1)

    img = np.expand_dims(img, axis=0)

    img = Variable(torch.from_numpy(img).to(device).float())
    print(img.shape)

实例化Alexnet模型，并设置为预测模式。预测模式和训练模式的主要区别是，Dropout和BN层的行为不一样，比如预测模式时，Dropout会让全部数据通过，训练模式时会按照设定值随机丢失一部分数据。对原始数据进行预测，预测的标签值为388，表示为熊猫。

    # 使用预测模式 主要影响droupout和BN层的行为
    model = models.alexnet(pretrained=True).to(device).eval()
    # 获取分类标签
    label = np.argmax(model(img).data.cpu().numpy())
    print("label={}".format(label))

设置仅输入数据可以计算梯度并被反向传递调整，模型的其他参数锁定不修改。在PyTorch中通过设置requires_grad值即可完成上述设置。优化器torch.optim.Adam只可调整输入数据img.

# 图像数据梯度可以获取
    img.requires_grad = True

    # 设置为不保存梯度值 自然也无法修改
    for param in model.parameters():
        param.requires_grad = False

    optimizer = torch.optim.Adam([img], lr=0.01)

下面进行迭代计算，优化的目标是让损失函数（或称目标函数）最小化。迭代过程中优化器不断调整输入数据img，这一过程需要手工调用loss.backward进行反向传递，通过optimizer.step调整img。整个迭代过程的退出条件是达到最大迭代次数或者img预测值达到预期。

# 设置定向攻击，攻击目标的标签值为288 最大迭代次数为100
    loss_func = torch.nn.CrossEntropyLoss()
    epochs = 100
    target = 288
    target = Variable(torch.Tensor([float(target)]).to(device).long())

    for epoch in range(epochs):
        # 梯度清零
        optimizer.zero_grad()
        # forward + backward
        output = model(img)
        loss = loss_func(output, target)
        label = np.argmax(output.data.cpu().numpy())
        print("epoch={} loss={} label={}".format(epoch,loss,label))
        original_loss += [loss]
        adam_original_loss += [loss]
        epoch_range += [epoch]
        # 手动调用反向传递计算，更新原始图像
        loss.backward()
        optimizer.step()
image-20210617035413149

最后将对抗样本进行对比。

image-20210617035554026

FGM/FGSM算法 – 基于梯度的对抗样本算法

FGM，快速梯度算法，

算法原理

假设图片原始数据为$x$，图片识别的结果为$y$，原始图像上叠加细微的变化$\eta$，肉眼难以识别$\eta$，使用数学公式表示如下:
$$
\tilde x = x + \eta \
w^T\tilde x = w^T\tilde x + w^T\eta
$$
同时为了追求微小修改，可以将$\eta$与梯度的变化方向完全一致。
$$
\eta = sign(w)
$$
$sign函数$

image-20210617041640290

当x的维数为n时，模型的参数在每个维度的平均值为m，η的无穷范数为$\varepsilon$，每个维度的微小修改与梯度函数方向一致，累计的效果为$nm\varepsilon$。当数据的维度n很大时，虽然η非常小，但是累计的效果却可以较大，该效果作用到激活函数上，有可能对分类结果产生较大影响。例如一般的图像数据维度都很大，即使是非常小的[32，32，3]的图片，维度也达到了3072，假设ε非常小，仅为0.01，m为1，那么累计的效果为30.72。同时，因为每一次的修改都与梯度函数方向一致，也就使FGM算法，可以进行定向攻击。

生成对抗样本

具体流程如下图：

image-20210617041817177

首先通过前向计算，获取img对应的输出，计算出当前对应的标签id。

#图像加载以及预处理
image_path="picture/cropped_panda.jpg"
orig = cv2.imread(image_path)[..., ::-1]
orig = cv2.resize(orig, (224, 224))
img = orig.copy().astype(np.float32)

mean = [0.485, 0.456, 0.406]
std = [0.229, 0.224, 0.225]
img /= 255.0
img = (img - mean) / std
img = img.transpose(2, 0, 1)

img=np.expand_dims(img, axis=0)

img = Variable(torch.from_numpy(img).to(device).float())
print(img.shape)

#使用预测模式 主要影响droupout和BN层的行为
model = models.alexnet(pretrained=True).to(device).eval()
image-20210617043029125

然后手工清零梯度值并触发反向传递，计算出对应的梯度值img.grad.data。使用该梯度值，按照FGM的算法取sign值并乘以，使用该值更新img.data

for epoch in range(epochs):

    # forward + backward
    output = model(img)

    loss = loss_func(output, target)
    label=np.argmax(output.data.cpu().numpy())

    print("epoch={} loss={} label={}".format(epoch,loss,label))

    #如果定向攻击成功
    if label == target:
        print("")
        break

    #梯度清零
    optimizer.zero_grad()
    #反向传递 计算梯度
    loss.backward()

    img.data=img.data-e*torch.sign(img.grad.data)

经过22轮迭代后，攻击成功，对抗样本对应的预测标签为288。

image-20210617043109986

基于梯度的对抗样本算法还有：

  • DeepFool
  • JSMA
  • C&W

三 防御方法

对抗样本的鲁棒性

上面，我们主要研究了样本本身的鲁棒性。对于白盒攻击，我们可以主要通过基于优化的对抗样本生成攻击和基于梯度的对抗样本算法攻击，来降低样本的鲁棒性，从而达到定向或无定向攻击。同样，对抗样本自身也有鲁棒性问题。

这里主要介绍图像对比度和亮度对鲁棒性的影响。

对比度和亮度对鲁棒性的影响

可以通过修改像素的方式来改变图像的对比度和亮度，公式为：
$$
f(x\prime) = \alpha f(x) + \beta
$$
其中α调整的是对比度，值越大对比度越大；β调整的是亮度，值越大亮度越大。

对比度对鲁棒性的影响

下面我们调整对抗样本的亮度，调整范围为–200到+200，每次增加10，并记录下亮度调整值和对抗样本预测为熊猫及定向攻击目标的概率，对抗样本使用FGM算法生成，定向攻击目标标签为288，要求概率大于80%

#验证亮度对  对抗样本的影响
std_range = range(-200,200,10)
adv_288_pro = []
adv_388_pro = []

for i in std_range:

    brightness_adv_img=np.clip((adv.copy()+i),0,255)

    pro_388=infer_img(brightness_adv_img.copy(),388)
    pro_288=infer_img(brightness_adv_img.copy(),288)
    print("std={} pro[388]={} pro[288]={}".format(i,pro_388,pro_288))
    adv_288_pro += [pro_288]
    adv_388_pro += [pro_388]

fig, ax = plt.subplots()
ax.plot(np.array(std_range), np.array(adv_288_pro), 'b--', label='Probability of Class 288')
ax.plot(np.array(std_range), np.array(adv_388_pro), 'r', label='Probability of Class 388')

legend = ax.legend(loc='best', shadow=True, fontsize='large')
legend.get_frame().set_facecolor('#FFFFFF')

plt.xlabel('Brightness Change Range')
plt.ylabel('Probability')
plt.show()
image-20210617052228372

上图,横轴代表亮度调整值，纵轴代表预测概率，实线代表对抗样本预测为熊猫的概率，虚线代表对抗样本预测为定向攻击目标的概率。我们假设概率大于50%时，分类结果可信，可见在该案例中，亮度调整范围小于–40或者大于10时，对抗样本定向攻击失效。当亮度调整范围小于–50或者大于40时，对抗样本预测为定向攻击目标的概率几乎为0。当亮度调整范围大于–90并且小于-50时，模型可以把对抗样本识别为熊猫，没有被欺骗。

下面我们调整原始图像和对抗样本的亮度，调整范围为–200到+200，每次增加10，并记录下亮度调整值和预测为熊猫对应标签的概率，对抗样本使用CW算法生成，定向攻击目标标签为288，要求概率大于80%

import matplotlib.pyplot as plt
#综合分析亮度对 对抗样本和正常图片分类的影响
std_range = range(-200,200,10)
original_pro = []
adv_pro = []

for i in std_range:

    brightness_adv_img=np.clip((adv.copy()+i),0,255)

    pro_388=infer_img(brightness_adv_img.copy(),388)
    adv_pro+= [pro_388]

    brightness_img=np.clip((orig.copy()+i),0,255)
    pro=infer_img(brightness_img.copy(),388)
    original_pro += [pro]

    print("std={} adv_pro[388]={} original_pro[388]={}".format(i,pro_388,pro))


fig, ax = plt.subplots()
ax.plot(np.array(std_range), np.array(adv_pro), 'b--', label='Probability of Adversarial')
ax.plot(np.array(std_range), np.array(original_pro), 'r', label='Probability of Original')

legend = ax.legend(loc='best', shadow=True, fontsize='large')
legend.get_frame().set_facecolor('#FFFFFF')

plt.xlabel('Brightness Change Range')
plt.ylabel('Probability')
plt.show()
image-20210617052951809

横轴代表亮度调整值，纵轴代表预测概率，实线代表原始图片预测为熊猫的概率，虚线代表对抗样本预测为熊猫的概率。我们假设概率大于80%时，分类结果可信，可见在该案例中，亮度调整范围大于–90且小于-50时，可以抵御对抗样本攻击，把原始图片和对抗样本均识别为熊猫

下面我们调整对抗样本的对比度，调整范围为0.1到+2.0，每次增加0.1，并记录下对比度调整值和对抗样本预测为熊猫及定向攻击目标的概率，对抗样本使用CW算法生成，定向攻击目标标签为288，要求概率大于80%。

#验证对比度对  对抗样本的影响
std_range = np.arange(0.1,2.0,0.1)
adv_288_pro = []
adv_388_pro = []

for i in std_range:

    contrast_adv_img=np.clip((adv.copy()*i),0,255)

    pro_388=infer_img(contrast_adv_img.copy(),388)
    pro_288=infer_img(contrast_adv_img.copy(),288)
    print("std={} pro[388]={} pro[288]={}".format(i,pro_388,pro_288))
    adv_288_pro += [pro_288]
    adv_388_pro += [pro_388]

fig, ax = plt.subplots()
ax.plot(np.array(std_range), np.array(adv_288_pro), 'b--', label='Probability of Class 288')
ax.plot(np.array(std_range), np.array(adv_388_pro), 'r', label='Probability of Class 388')

legend = ax.legend(loc='best', shadow=True, fontsize='large')
legend.get_frame().set_facecolor('#FFFFFF')

plt.xlabel('Contrast Change Range')
plt.ylabel('Probability')
plt.show()
image-20210617053426263

横轴代表对比度调整值，纵轴代表预测概率，实线代表对抗样本预测为熊猫的概率，虚线代表对抗样本预测为定向攻击目标的概率。我们假设概率大于50%时，分类结果可信，可见在该案例中，对比度调整范围小于0.6或者大于1.4时，对抗样本定向攻击失效。

import matplotlib.pyplot as plt
#综合分析对比度对 对抗样本和正常图片分类的影响
std_range = np.arange(0.1,2.0,0.1)
original_pro = []
adv_pro = []

for i in std_range:

    contrast_adv_img=np.clip((adv.copy()*i),0,255)

    pro_388=infer_img(contrast_adv_img.copy(),388)
    adv_pro+= [pro_388]

    contrast_img=np.clip((orig.copy()*i),0,255)
    pro=infer_img(contrast_img.copy(),388)
    original_pro += [pro]

    print("std={} adv_pro[388]={} original_pro[388]={}".format(i,pro_388,pro))


fig, ax = plt.subplots()
ax.plot(np.array(std_range), np.array(adv_pro), 'b--', label='Probability of Adversarial')
ax.plot(np.array(std_range), np.array(original_pro), 'r', label='Probability of Original')

legend = ax.legend(loc='best', shadow=True, fontsize='large')
legend.get_frame().set_facecolor('#FFFFFF')

plt.xlabel('Contrast Change Range')
plt.ylabel('Probability')
plt.show()
image-20210617094431472

横轴代表对比度调整值，纵轴代表预测概率，实线代表原始图片预测为熊猫的概率，虚线代表对抗样本预测为熊猫的概率。我们假设概率大于50%时，分类结果可信，可见在该案例中，无法做到同时兼顾对抗样本和正常图片的识别。

参考链接

《AI安全之对抗样本入门》 兜哥

《床长人工智能教程》 床长

暂无评论

发送评论 编辑评论 


				

			

						

				

					

						

							

								
							

							
						

					

				

				

					

						

							

								
							

							
						

					

				

				

					

						

							

								
							

							
							
													

					

				

			

			
			

				

					
				

			

				

											

							
							
						

																				
					
											
						

	

		
|´・ω・)ノ
ヾ(≧∇≦*)ゝ
(☆ω☆)
（╯‵□′）╯︵┴─┴
￣﹃￣
(/ω＼)
∠( ᐛ 」∠)＿
(๑•̀ㅁ•́ฅ)
→_→
୧(๑•̀⌄•́๑)૭
٩(ˊᗜˋ*)و
(ノ°ο°)ノ
(´இ皿இ｀)
⌇●﹏●⌇
(ฅ´ω`ฅ)
(╯°A°)╯︵○○○
φ(￣∇￣o)
ヾ(´･ ･｀｡)ノ"
( ง ᵒ̌皿ᵒ̌)ง⁼³₌₃
(ó﹏ò｡)
Σ(っ °Д °;)っ
( ,,´･ω･)ﾉ"(´っω･｀｡)
╮(╯▽╰)╭
o(*////▽////*)q
＞﹏＜
( ๑´•ω•) "(ㆆᴗㆆ)
😂
😀
😅
😊
🙂
🙃
😌
😍
😘
😜
😝
😏
😒
🙄
😳
😡
😔
😫
😱
😭
💩
👻
🙌
🖕
👍
👫
👬
👭
🌚
🌝
🙈
💊
😶
🙏
🍦
🍉
😣
Source: github.com/k4yt3x/flowerhd
	

	

		
颜文字
Emoji
小恐龙
花!
	


									

			

			
			
		

	






上一篇
下一篇 

                    

                    
			        推荐文章
		            

		            

							
CnHongke

							
							

							
密码保护：SQLI – lab – other

							
							

							
靶场复现 – VulnStack 0x02

							
							

							
THINKPHP 任意文件操作漏洞 & 任意代码执行漏洞 复现

							
							

							
MS 14-068 && CVE-2020-1472

							
							

							
Weblogic 漏洞复现

							
							

							
Fastjson 反序列化

							
							

							
xctf高校网络安全挑战赛-华为云专场

							
							

							
【读书节·荐书】